A Self-Supervised Learning Approach with Differentiable Optimization for UAV Trajectory Planning

While Unmanned Aerial Vehicles (UAVs) have gained significant traction across various fields, path planning in 3D environments remains a critical challenge, particularly under size, weight, and power (SWAP) constraints. Traditional modular planning systems often introduce latency and suboptimal performance due to limited information sharing and local minima issues. End-to-end learning approaches streamline the pipeline by mapping sensory observations directly to actions but require large-scale datasets, face significant simto-real gaps, or lack dynamical feasibility. In this project, we propose a self-supervised UAV trajectory planning pipeline that integrates a learning-based depth perception with differentiable trajectory optimization. A 3D cost map guides UAV behavior without expert demonstrations or human labels. Additionally, we incorporate a neural network-based time allocation strategy to improve the efficiency and optimality. The system thus combines robust learning-based perception with reliable physicsbased optimization for improved generalizability and interpretability. Both simulation and real-world experiments validate our approach across various environments, demonstrating its effectiveness and robustness. Our method achieves a 31.33% improvement in position tracking error and 49.37% reduction in control effort compared to the state-of-the-art.

Planning Pipeline

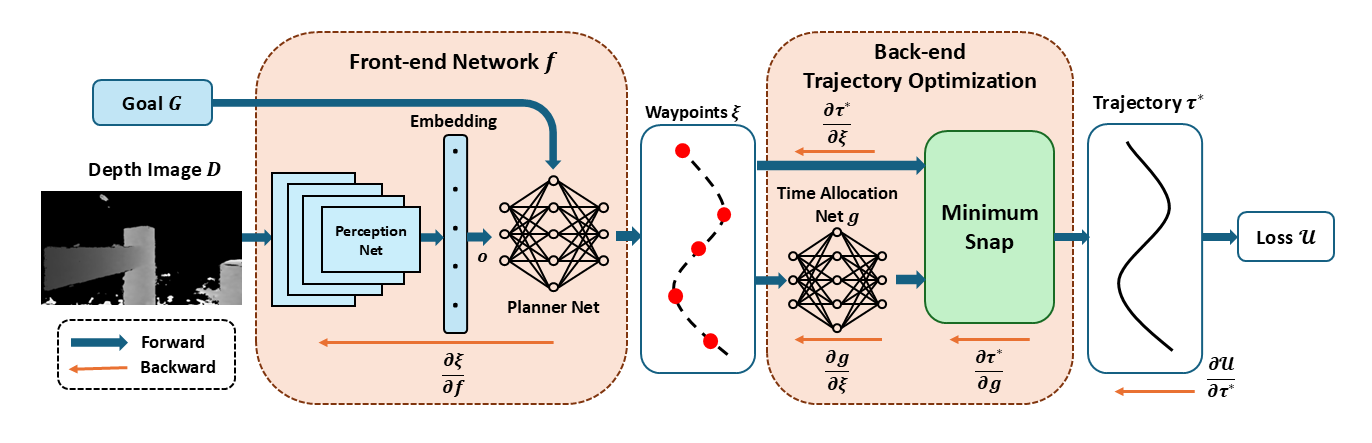
Our method takes only depth images as input, and directly outputs trajectories through end-to-end pipeline. Each module is fully differentiable, enabling gradient backpropagation through effective joint training. Specifically, a front-end network first predicts key waypoints from the input depth image. Then, back-end trajectory optimization module generates an optimal trajectory based on these waypoints. Additionally, we introduced a time allocation network to handle the challenging timing problem, ensuring both real-time performance and trajectory optimality. Compared to other approaches, our method is fully self-supervised thanks to our 3D cost map. Moreover, with iterative trajectory optimization, we can incorporate inequality constraints, further enhancing its practical applicability.

Experiment Results

Navigation in various simulation environments

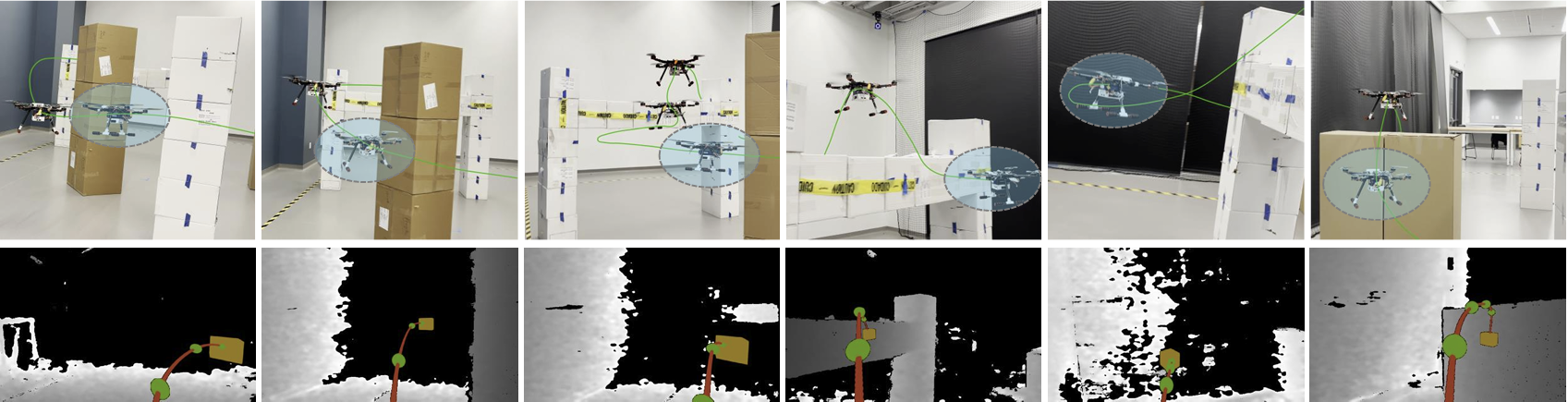
Real-world obstacle avoidance in 3D complex environment

Video

@misc{jiang2025selfsupervised,
      title={A Self-Supervised Learning Approach with Differentiable Optimization for UAV Trajectory Planning}, 
      author={Yufei Jiang and Yuanzhu Zhan and Harsh Vardhan Gupta and Chinmay Borde and Junyi Geng},
      year={2025},
      eprint={2504.04289},
      archivePrefix={arXiv},
      primaryClass={cs.RO},
      url={https://arxiv.org/abs/2504.04289}, 
}